物理量には「単位」があります。
例えば、重さなら ${\rm kg}$(キログラム)、長さなら ${\rm m}$(メートル)、時間なら ${\rm s}$(秒) などです。もちろん、重さを ${\rm g}$(グラム) で測っても良いですし、長さを ${\rm cm}$(センチメートル)、時間を ${\rm h}$(1時間=60分)で測っても良いです。
それぞれ値は変わっても「次元」は変わりません。重さという次元、長さという次元、時間という次元です。
ここでは簡単のために、重さは ${\rm kg}$、長さは ${\rm m}$、時間は ${\rm s}$ で測ることにしましょう。
何か問題を解いている時に、計算の中に例えば($h$ を高さ、すなわち、長さの次元を持ったもの、$g$ を重力加速度とします。)
$$h + g$$
という式が出てきたとします。これは、どこかで計算が間違っているという「サイン」です。
それは、違う「次元」の量を「足して」いるからです。
例えば、1 時間と1 秒を足したら幾つになりますか?と聞かれたら困りますよね。
足し算や引き算は「同じ次元を持った量同士」でないと意味がありません。
ですから、先のような項はどこかで絶対に間違っています!
ちなみに、重力加速度の次元はどうなるでしょうか?加速度の次元ですから距離/(時間)$^2$です。つまり ${\rm m}/{\rm s}^2$ となります。
このように、計算の途中で計算ミスを見つけることにも役に立ちますし、最後に出した答えが間違っていないか確かめることも出来ます。
問題で「時間」を聞かれているのに、最後の出てきた答えが「時間」の「次元」を持っていなかったとしたら、絶対に間違っていますよね。
具体的に、どういう風に使えるか実例を見てみましょう。
これは2022年度の物理の本試験の第4問の問1の選択肢です。
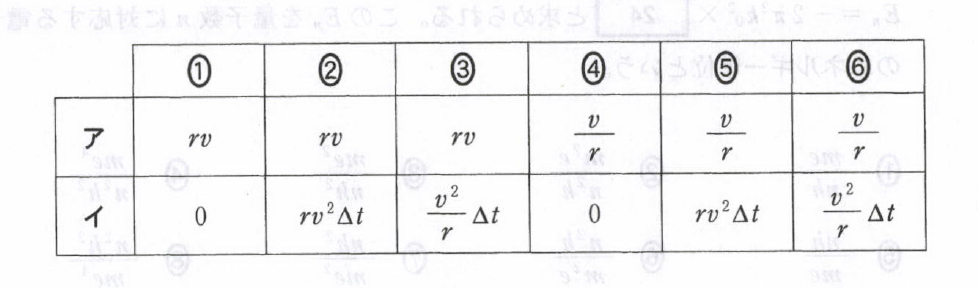
問題文によると(ア)は角速度、(イ)は速度の差、すなわち速度を選びなさいという問題です。
角速度の次元は $1/{\rm s}$ です。
そうすると、$\frac{v}{r}$ はちゃんと角速度の次元を持っていることが分かります。実際
$$\frac{{\rm m}/{\rm s}}{\rm m} = 1/{\rm s}$$
となります。しかしながら、$r v$ は角速度の次元を持っていません。
この段階で、選択肢のうち①、②、③が外れます。
次に(イ)の選択肢を見てみましょう。$\frac{v^2}{r} \Delta t$は速度の次元を持っています。実際に
$$\left({\rm m}/{\rm s}\right)^2 \times {\rm s}/{\rm m} = {\rm m}/{\rm s}$$
となります。しかし、$r v^2 \Delta t$ は速度の次元を持っていません。
これで選択肢⑤が外れます。
結局、④と⑥が残ります。
次元だけの考察で問題文を読まなくても、選択肢のうちの 2/3 を除外することが出来ました。
少し問題を読んで、速度の変化が 0 でないことを確かめれば、答えが⑥であることが分かります。
実際に、この問の答えは⑥です。
このように、単位を見るだけで、問題文を読まなくても、ある程度答えの候補を絞ることが出来ます。
時には単位だけの考察で、答えを選ぶことさえあります。
これから、問題を解く時には「単位」に着目してみませんか?